
When the short side is 1, the long side is 1 2+5 2, so: The square root of 5 is approximately 2. The ratio is 1: 0.618: 1 so the width of the first and third vertical columns will be 1, and the width of the center vertical column will be 0.618. If “a” is the width and “a + b” the length of the rectangle, then the golden ratio is \(\frac-a\). That rectangle above shows us a simple formula for the Golden Ratio. Simply, the golden ratio (also called the golden rectangle and golden mean) is a shape with a proportion of 1 to 1.618. Recall that a ratio is the relationship between two quantities, represented generally as a fraction. Seen throughout architecture and nature, the golden rectangle is a rectangle whose sides are in what is called the “golden ratio”. As observers we can appreciate the final result by overlaying shapes of Divine Proportion to increase our awareness of the overall dynamics.This handy calculator will determine the length of either side of the golden rectangle as well as the area, if the other side is known. And if you were to expand it out, it's an irrational number, 1.61803, and it just goes on and on and on forever, but there's some very neat mathematical. Whether this is done according to some inner sense of harmony or it is calculated is something only the artist will know. This means that the width of the first column and third column will be 1, while the width of the center column. In order to balance the elements of color, movement, and content within the shape of the canvas, key attention points or shapes are placed in certain relationships with other key points. The Golden Ratio for a photograph is 1: 0.618: 1. The divine proportion can be implemented to divide a canvas according to overall design and content, draft a composition of the whole artwork or its parts, balance tonal values or colors. The golden rectangle is a rectangle whose sides are in the golden ratio, that is (a + b)/a a/b, where a is the width, a + b is the length of the rectangle, and is the golden ratio: (1+5)/2. There are unlimited considerations for an artist to use the golden ratio. One of the most famous of all geometric figures is the Golden Rectangle, which has the ratio of length to width equal to the Golden Section. So, understanding and using the golden ratio is important for any artist. The relationship of balance, principles of harmony, and symmetry all present in the best works of fine art. Show that the arithmetic mean, geometric mean and harmonic mean of a and b can be the lengths of the sides of a right-angles triangle if and only if a bx3. The inverse of phi (1/) is noted with capital phi () and is equal to 0.6180. What we perceived as beautiful, well-proportionate and balanced in nature, finds its way into fine art, following the same rules of divine proportions that universe has.
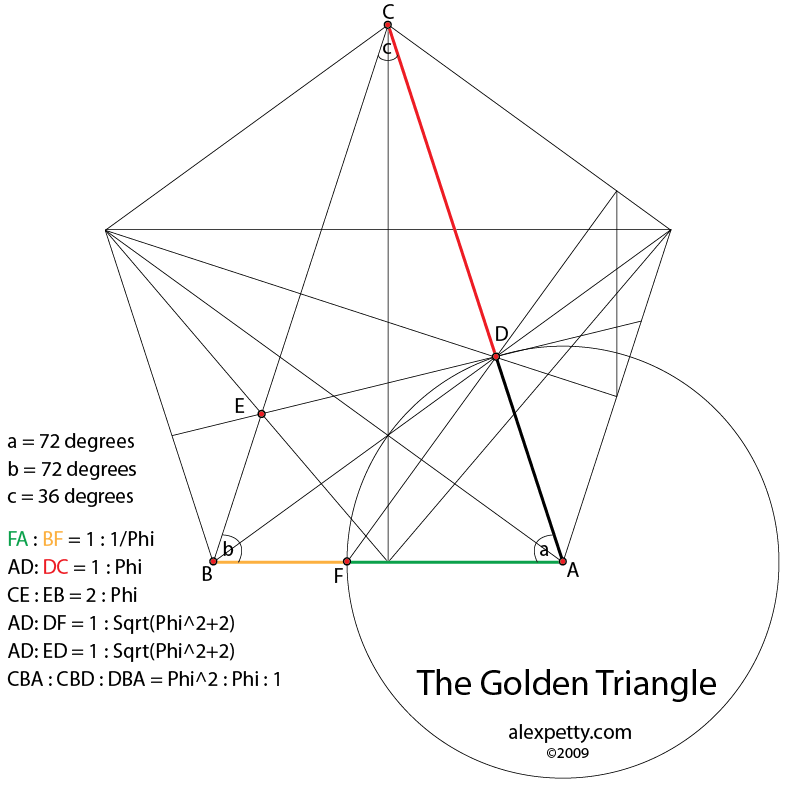
Golden Ratio in ArtĪrt reflects the nature and the inner world of an artist. In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio,, which is (the Greek letter phi), where is approximately 1.618. You often get this number by taking the ratio of two quantities in nature (i.e., by dividing one quantity by the other). The value of the golden ratio, which is the limit of the ratio of consecutive Fibonacci numbers, has a value of approximately 1.61803.


 0 kommentar(er)
0 kommentar(er)
